ekology@tut.by
Фи-треугольник - геометрия мироздания и инструмент познания
Материя - есть возбужденное состояние динамической геометрии…
Геометрия предопределяет законы движения материи…Уиллер Дж. Предвидение Эйнштейна
Часть 1. Фи-треугольник - фигура Золотого сечения
1. Определение, построение.
2. Основные соотношения. Фи-треугольник и пирамиды.
1. Определение, построение.
Иоган Кеплер говорил, что геометрия владеет двумя сокровищами - теоремой Пифагора и золотым сечением, и если первое из них можно сравнить с мерой золота, то второе - с драгоценным камнем.
Напомним определение
Золотое сечение - деление отрезка на две неравные части
a и b (рис.1) таким образом, чтобы большая часть а была средним пропорциональным
между всем отрезком (a+b) и меньшей частью b, или, другими словами:
такое деление целого на две неравные части, при котором большая часть
так относится к целому, как меньшая часть к большей:
|
Рис. 1 |
a + ba
b
a |
Это уравнение имеет два корня, один из которых - положительный корень (1+sqrt(5))/2 - и есть численное значение золотого сечения.
Анализ большинства шедевров мирового искусства показывает, что их основное построение основано на пропорциях Золотого сечения.
Строим ЗОЛОТОЕ СЕЧЕНИЕ - по классическому варианту
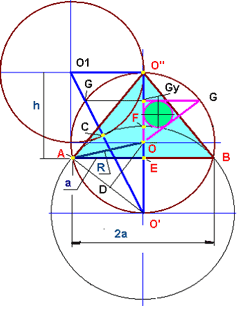
1. Откладываем произвольный отрезок O O1. (рис.2)
2. Отрезок такой же длины откладываем перпендикулярно вниз - OO .
3. Радиусом R = O O1 = OO проводим окружности с центрами в точках О и О1.
Скажем заранее, что окружность с центром в т.О и радиусом R будет в
дальнейшем основной в рассматриваемой комбинации фигур….
|
Рис. 2 |
Эта
версия статьи предназначена для особо интересующихся
математикой и доказательствами производимых выводов, а также владеющих
аппаратом решения геометрических задач. Все приводимые значения
просчитаны с точностью до 11-го знака. Это делается для того,
чтобы убедиться в абсолютной точности заключений. Кроме того,
достаточно много оказывается величин, лежащих друг к другу чрезвычайно
близко.
СПРАВОЧНЫЕ
ЗНАЧЕНИЯ 1. Число фи
Ф = 1,618033989…, определяем его (абсолютно точно
) как: ((корень кв. (5) +1) /2 ) 2. Число ф
= 1/Ф = 0,618033989… 3. Число пи = 3,141592654… Углы и их значения будем обозначать < |
Величину R примем равной 1. R = 1
Составим
таблицу, в которую будем заносить все полученные по ходу вычислений
результаты. Курсивом при этом выделены значения, полученные позже их
занесения в таблицу.
Далее будем заносить многие результаты без комментариев, но с указанием
примененной формулы.
4. Соединяем т.О1 с концом диаметра O'.
|
Параметр |
Формула |
Значение |
ПРИМЕЧАНИЕ |
||
|
углы - в рад, длины -- в числах «R» |
углы - в град, длины -- в числах «а» |
Для колонки 3 |
Для колонки 4 |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
R |
= OO” = ОА = O1C |
1 |
1,029085514 |
|
Ф 1,5 |
|
O1O' |
(O O12+ O'O 2 ) ½ |
2,236067977 |
2,301105163 |
2Ф - 1 |
|
|
O'C = O' F=R’ |
O' O1 - O1C |
1,236067977 |
1,27201965 |
2Ф - 2 |
SQRT (Ф) |
|
FO |
O'O - O' F |
0,763932023 |
0,786151378 |
|
1/(SQRT (Ф)) |
Отрезки O'O и O' F; O' F и FO относятся соответственно друг к другу в точном значении Золотой пропорции :
| O'O
/ O' F O' F / FO |
1,618033989 |
5. Проведём перпендикуляр
ОD к отрезку O'A -
Т.к. точки O' и А лежат на окр-ти, то тр-к O'AO - равнобедренный,
|
1 |
2 |
3 |
4 |
5 |
6 |
|
AD = O' D |
R’/ 2 |
0,618033989 |
0,636009825 |
ф |
2 /(SQRT(Ф)) |
|
< DAO = <DO'O |
arccos (AD/ R) |
0,904556894 |
51,827292373 |
|
|
6. Из т. А проведём перпендикуляр AB к O'O . Отрезок АЕ = AB/2 обозначим а
|
AE = a |
O'A*sin<DO'O |
0,971736544 |
1 |
|
|
|
O' E |
O'A * cosDO'O |
0,763932023 |
0,786151378 |
|
1/ (SQRT(Ф)) |
|
EO |
R - O' E |
0,236067977 |
0,242934136 |
1/ (2Ф + 1) |
ЕО = 1/( 4R ) |
|
<EAO' |
90 - <DO'O |
0,666239432 |
38,172707627 |
|
|
|
<EAO |
<DAO - <EAO' |
0,238317462 |
13,654584746 |
|
|
|
R |
a / (cos(<EAO)) |
1,029085514 |
1 |
Ф 1,5 |
|
|
EO |
OE + R |
1,236067977 |
1,27201964951407 |
2 / Ф |
SQRT(Ф) |
|
tg <EAO |
EO /AE |
1,27201964951407 |
|
SQRT(Ф) |
|
|
<EAO |
|
0,904556894 |
51,827292373 |
|
|
7.
Соединим т. А и O ; B и O . Образовался равнобедренный, вписанный
в окружность с центром в т.О, треугольник ABO , который и будет
являться главным предметом нашего пристального внимания и, собственно,
причиной написания данной статьи. Полученный треугольник (назовем его
фи-треугольник , хотя с полным основанием его можно было
бы называть и золотым), обладает в сочетании с описанной вокруг него
окружностью с центром в т.О, многими замечательными свойствами, особенности
которых будем рассматривать ниже по ходу повествования. Углы EAO ,
AO E, EAO будем считать главными в данной комбинации и обозначим
соответственно их:
α, β, γ .
Определим основные параметры треугольника ABO”. Однако мы почти все их уже и вычислили. Подытожим.
|
|
Значения в градусах |
обозначения |
|
<EAO – главный угол. |
51,8272923729877… |
α |
|
<AO E 90о – EAO” |
38,1727076270123… |
β |
|
<AO” E – угол при вершине = 2 β |
76,3454152540245… |
|
|
<EAO - AO E |
13,6545847459755… |
γ |
Радиус описанной окружности: R = a / (cos(<EAO)) = 1,029085514… = Ф 1,5
При этом заметим, что угол γ абсолютно совпадает по значению с углом ЕАО !Фи-треугольник (ABO”) построен. Он является вертикальным сечением пирамиды, в основании которой лежит квадрат со стороной AB, и высотой EO”.
Чтобы не путаться в дальнейшем с двумя рядами значений для линейных размеров, договоримся, что основной единицей измерения будем считать длину «а», принятую за «1» отрезка АЕ (полуоснование фи-треугольника.). Это всегда будет колонка цифр № 4. Хотя в таблице будем давать значения по обоим рядам (в том числе – и в числах, выраженных через количество «R» – колонка цифр № 3).
Основание треугольника (сторона основания пирамиды) АВ = 2а, или просто = 2.
Высота треугольника h = EO” = (Ф) 0,5 = 1,27201964951407a
Этому же числу равен и тангенс главного угла α.
Сторона треугольника AO” (обозначим ее буквой « g » - гипотенуза).
|
G |
а / cos α |
1,57230275551485 |
1,61803398875 |
2 / ( Ф) 0,5 |
Ф |
Заметьте: пи / 2 = 1,5707963267949
g – пи / 2 = 0,00150642871995, или 0,096% !
Один и тот же параметр (g) в двух разных единицах измерения дает одновременно «фи» и «пи»!
Число 1,57230275551485 выражается через фи соотношением: 2 / ( Ф) 0,5.
2. Основные соотношения. Фи-треугольник и пирамиды.
Теперь посмотрим на угол α = 51,8272923729877 О
Угол наклона боковых граней Великой пирамиды: αп=51,8427734126309О
Разница αп – α составляет 56 сек, или 0,03% !!!
В пирамиде гипотенуза g является высотой её боковой грани.
Теперь сравним этих два угла «α» с тем вариантом, когда угол наклона пирамиды определяло бы строго число «пи».
В последнем случае «α» = arctg (4/пи) = αпи = 51,8539740127775О
Разница αпи – α : 0 град 1 мин 36 сек, или 0,05 % !!
Разница αпи – αп = 40 сек, или 0,02% !!!
Сравнивая расхождения в углах наклона, отмечаем, что «среднее» положение занимает реальная пирамида (Хуфу - Хеопса). Наибольший угол с основанием составляли бы грани пирамиды, у которой присутствуют зависимости от «пи», и наименьший – от «фи». Принимая Великую пирамиду за «центр», определяем, что отклонение от её главного угла на 56 угловых секунд в меньшую сторону даёт пирамиду с «фи-треугольником» в вертикальном сечении, а на 40 сек в большую сторону, соответственно, – пирамиду с «пи-треугольником».
Да простит нас требовательный читатель за некую вольность в присвоении названий и возможность прочих негрубых неточностей. Думаю, что со временем нечёткие моменты отшлифуются. Сейчас хотелось бы просто донести до Вас суть излагаемого материала.
Таким образом, отклонения от значения угла наклона боковых граней в теле реальной пирамиды в ту и другую стороны отличаются всего лишь на 16 сек друг от друга.
Мы постоянно задаёмся вопросом: как могли строители египетских пирамид достичь столь высоких показателей точности и качества да при внушительных размерах строящегося объекта? В результате всё большего количества поразительных находок в этих артефактах наша цивилизация вынуждена признать, что древние обладали высочайшими технологиями, а следовательно, и степенью развития научных знаний.
Но тогда: раз такие достижения действительно имели место, то как «они» могли не знать числа «пи»? А такое мнение достаточно прочно утвердилось среди исследователей древней цивилизации. Действительно, в основу пирамиды положено соотношение 22/7 [Лемезурье. “Великая пирамида расшифрована”].
Сравните значения:
пи = L / D = 3,141592654…
(где L – длина окружности, D – ее диаметр)
22/7 = 3,142857143…
22/7 – пи = 0,00126448925… = 0,0004%
Если же исходить из числа «фи», то примерное значение «пи» будет равно:
4/ (кв. корень(Ф)) = 3,144605511…
Но ведь точно просчитать значение числа «пи» совсем несложно даже с меньшим уровнем знаний, чем обладали египтяне. Достаточно более-менее точно измерить значения длины круга и его диаметр и вычислить «пи» как их отношение.
Не сознательно ли допущено такое отклонение, и выбрано значение угла наклона, близкое к среднему значению, чтобы обратить внимание потомков на взаимосвязь между великими числами «пи» и «фи»??? А числа «22» и «7» так же играют весьма значительную роль во многих культах во все времена, в том числе, и у египтян. А ведь взяты именно они за основу. И это, очевидно, отнюдь не случайный выбор и, тем более, не недостаток знаний элементарной геометрии.
Числа фи, пи и 22/7, вернее основанные на них три возможных варианта пропорций пирамиды, и возникающие на их основе соотношения могут отображать и три различных аспекта знаний инженеров пирамиды, например: законы мироздания, ход истории и географию Земли и Космоса.
В этой статье не рассматривается вариант, применяемый древними китайцами для вычисления числа «пи» как соотношение 355/113.
С другой стороны, Валерий Дёмин в своей работе Тайны Вселенной говорит так: Подмеченная закономерность была выведена Ю.А.Абрамовым ещё в 1987 году, за истекшие 10 лет он увидел, что ряд продолжается и в сторону с отрицательными степенями.... Итого получается 22(!!!) уровня иерархии строения Вселенной...
Далее: «Вселенная – йок каб (буквально «над землёй») рисовалась древним майя (связь между египетскими и мексиканскими пирамидами сегодня общепризнанна, - ГА) в виде слоистой иерархии миров: над землёй находилось тринадцать небес, а под землёй – девять этажей преисподни».
А число 7 общепризнанно является священным для многих народов. По сути дела, весь Космос имеет семеричное строение.
Вот какие любопытные заключения выдает нам Александр Волков в работе «МАТЕМАТИКА КАК ЕДИНЫЙ ИСТОЧНИК МИРОВЫХ РЕЛИГИЙ»
Семёрка
это первое из простых чисел, которое можно назвать истинно простым.
Рассмотрим предшествующие семёрке простые числа. Единица - простое число.
Простые делятся на себя и на единицу. Но в этом случае на единицу и
значит на себя. Т.е. у единицы всего один делитель, а у всех остальных
простых чисел по два делителя. Следующее простое число 2 .
Его отличает от всех других простых чётность. Тройка - Авель.
Вы только что прочитали о его отличительном признаке, цифровом корне
равном ему самому. Возможно, древнегреческий миф о Нарциссе, вечно любующемся
своим отражением, это рассказ о том же самом числе три и
об отражающем его цифровом корне 3 , единственном в своём
роде простых . Такая исключительность отражения и служит
Нарциссу поводом для самолюбования. Последнее перед семёркой простое
число 5 . Единственное из простых чисел, оканчивающееся на
пять. Простые числа оканчиваются любой нечётной цифрой, кроме пятёрки.
А вот седьмый от Адама Енох уже ничем не отличается от всех
последующих простых, за что и вознесён. У числа 7 два делителя, как
у всех простых, кроме единицы; оно нечётное, как все простые, кроме
двойки; его корень 7 несут в себе простые 43, 61, 79, 97
и т.д.; на 7 оканчиваются простые 17, 37, 47, 67, 97 и т.д.
Есть и другая причина, по которой номер Еноха заслуживает особых отличий.
Семёрка скрывает в себе все шесть цифровых корней простых чисел. Если
при делении на семь в ответе будет дробное число, то вы увидите, что
в дробном остатке циклически повторяются эти цифровые корни: …1,4,2,8,5,7.
Енох как бы подсказывает, что дроби получающиеся в результате деления
одного натурального числа на другое всегда будут цикличны. Это значит,
что на обычном калькуляторе операцию деления можно производить с любой
точностью. Именно Енох помог мне открыть новый алгоритм отыскания
простых чисел в НЧР (натуральный числовой ряд - ГА), который много проще
общеизвестного.
Кроме того, Енох хранит главный библейский ключ, но об этом в
своё время. Возможно, и с вознесением пророка Илии связана в Библии
какая-то математическая задача.
Таким образом, напрашивается возможный вывод: двадцать два уровня иерархии Вселенной распределяются между семью первичными ячейками мироздания. При этом наполнение одной такой ячейки составляет число пи (т.к. 22/7 = пи)! С другой стороны, рассматривая отношения трёх этих чисел, логичным было бы предположить что 22/7 = пи - есть диаметр (вопрос, в каких единицах?) Вселенной, поскольку длина окружности L = пи*D! Ответы на все эти вопросы Человечеству ещё предстоит отыскать.
Но
вернемся к пирамиде.
Египетские жрецы сообщают Геродоту формулу пирамиды:.
- площадь боковой грани равна площади квадрата,
у которого длина стороны равна высоте пирамиды.
Забегая вперёд, скажем, что данной формуле в точности соответствует лишь вариант, рассматриваемый нами как основной, когда угол наклона боковых граней пирамиды равняется арктангенсу квадратного корня от числа фи . Т.е. в вертикальном сечении пирамиды лежит фи-треугольник .
Но как же тогда быть с реальными размерами пирамиды, угол наклона которой измерен неоднократно и большой точностью как равный тому значению, которое мы уже приводили? Я склонен считать данную тираду жрецов именно подсказкой для рассмотрения этих соотношений (фи) лишь в случае выяснения математических закономерностей. Но в реальных параметрах пирамиды заложен другой смысл: сакральный, исторический и т.п.!
Сейчас очень много говорят о связи чисел пи и фи , но автору не удалось отыскать чего-либо более-менее вразумительного. Некоторые исследователи склонны видеть в определяемом значении 4/ (кв. корень(Ф)) = 3,144605511… даже истинное значение числа пи , поскольку оно связано с основными физическими константами. Однако это не так - в силу указанных выше несложных возможностей определения числа пи с большой точностью и с тем значением, которое сегодня известно нам как классическое: пи = 3,141592654…
И хождение египтян по лезвию между пи и фи дает основание думать, что где-то за потайной дверцей параметров пирамиды они спрятали заветный золотой ключик , являющийся коэффициентом пересчёта между двумя главными числами мироздания!
Но продолжим далее:
Поскольку,
как мы уже показали, пропорции фи-треугольника весьма близки
к пропорциям реальной пирамиды, то и будем считать, что рассматриваем
Великую пирамиду. Однако целью автора является не только изучение скрытых
закономерностей Великой пирамиды, а и поиск некоего универсального инструментария,
алгоритма, способного облегчить процесс решения многочисленных задач
естествознания, включая упомянутый коэффициент пересчета между пи
и фи .
В подтверждение этого, опережая оформление соответствующей работы, скажу,
что уже удалось с помощью фи-треугольника найти оригинальный
способ построения Звезды Шри-Янтра , древнего геометрического
символа, используемого для медитации в различных школах тантризма. Решение
этой задачи является весьма непростым даже с помощью самых современных
компьютеров. Поэтому способ построения звезды нашими предками остается
тайной за семью печатями (А. Кулаичев Шри Янтра -
тайны геометрии ).
Малиновым
цветом на рис.1 выделен Золотой египетский треугольник -
ОGGy.
Он образован перпендикуляром GGy от точки G, лежащей на пересечении
окр. с ц. в т.О1; радиусом OG (R) и части вертикального радиуса от т.
О до пересечения с последним перпендикуляра GGy.
Доказательство. Рассматривается левый треугольник, зеркально симметричный выделенному малиновым цветом.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
<GO'O |
= <O'GO = arctg (R/2R) |
0,463647609 |
26,56505118 |
|
|
|
<GOO' |
180О - 2<GO’O |
2,214297436 |
126,8698976 |
|
|
|
O' G |
(R/sin<O’GO)* sin<GOO’ |
1,788854382 |
1,840884131 |
|
|
|
<O'GGy |
90O - <GO’O |
1,107148718 |
63,43494882 |
|
|
|
<OGGy |
<O’GGy – <O’GO |
0,643501109 |
36,86989765 |
|
|
|
<GOGy |
90O - <OGGy |
0,927295218 |
53,13010235 |
|
|
|
GGy |
O’G * sin<GO’O |
0,8 |
0,823268411 |
|
|
|
OG |
|
1 |
1,029085514 |
|
|
|
OGy |
R * cos<GOGy |
0,6 |
0,617451308 |
|
|
Отсюда - три стороны тр-ка OGGy находятся в пропорции золотого треугольника : 3; 4; 5.
На следующем этапе вычислений исследуем соотношения и зависимости в связи с точкой F. (см. рис. 2)
|
1 |
2 |
3 |
4 |
5 |
6 |
|
OF |
O' F - R |
0,236067977 |
0,242934136 |
= ЕО = 1 / ( 4R ) |
|
|
EF |
2EO |
0,472135955 |
0,485868272 |
= 1 / ( 2R ) |
|
Проверим соотношения:
H / FO 1,618033989
FO / EF
1,618033989
|
1 |
2 |
3 |
4 |
5 |
6 |
|
A Fg1а |
EF/ tgα |
0,371170332 |
0,381966011 |
|
= (1 / Ф)2 |
|
FFg1 |
a - AFg1а |
0,600566212 |
0,618033989 |
|
ф |
|
EFg1 |
|
0,763932023 |
0,786151378 |
|
EO’ !!! |
|
A / FFg1 |
|
1,618033989 |
Ф |
||
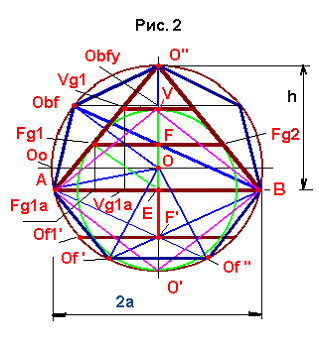 |
Для
простоты договоримся в дальнейшем, что проекции всех точек на горизонтальный
диаметр будем обозначать с индексом х , вертикальный
- у , на гипотенузу - с g , на основание -
с а .
Таким образом, точка F делит высоту h пирамиды строго в соответствии с золотой пропорцией Ф = 1,618033989… Длина же отрезка Fg1F определяется как a / Ф. Будем звать в дальнейшем отрезок Fg1Fg2 первой золотой линией , а отрезок FFg1 отрезком f 1 фи-треугольника. Вторая золотая линия будет определяться, по аналогии с первой, как: f 1 / Ф |
Вычислим значение f 2 (для простоты берем его половину, т.е FFg1...)
|
1 |
2 |
3 |
4 |
5 |
6 |
|
f 2 = V Vg1 |
FFg1 / Ф |
0,371170332 |
0,381966011 |
|
|
Тогда проекция т.Vg1 на основание а будет т. Vg1а
|
Vg1а A |
a - f 2 |
0,600566212 |
0,618033989 |
|
ф |
Высота расположения второй золотой линии будет:
|
E V |
Gг1аА * tgα |
0,763932023 |
0,786151378 |
= O'E !!! |
(ф) -1/2 |
|
F V |
EV - EF |
0,291796068 |
0,300283106 |
|
|
|
VO |
FO – F V |
0,472135955 |
0,485868272 |
= EF !!! |
1/ D |
Точка
V, в свою очередь, делит отрезок FO в золотой пропорции, а сама
линия f 2 является первой золотой линией уже для треугольника Fg1 Fg2
O !!!
Таким образом, пирамида делится золотыми линиями на три части, крайние
из которых имеют одинаковую высоту, а средняя находится с ними в золотой
пропорции в сторону уменьшения. Точки F и V назовем, соответственно,
первым и вторым фокусами треугольника. Но раз фокусы, то просится эллипс?
Очень интересно проверить было бы на соответствие реальную пирамиду. Имеет ли пирамида какие - либо признаки разделения на три области?
Мы
получили от т.Е три отрезка строго одинаковой длины: O' E, EFg1, EV,
что вызывает мысль провести вписанную в наш треугольник окружность с
центром в т.Е и радиусом R1 = O' E (выделена зелёным цветом).
Но об этом мы поговорим в дальнейшем.
Проведём
луч BF до пересечения с основной окружностью. Точку пересечения обозначим
Obf.
Определим теперь угол подъёма <ЕBF
|
1 |
2 |
3 |
4 |
5 |
6 |
|
<EBF |
arctg (EF/a) |
0,452278447 |
25,91364619 |
= α / 2 |
|
|
<OBF |
<EBF - < γ |
0,213960985 |
12,259061441 |
Отличается от α/ 4 |
|
Так как отрезок BF является биссектрисой угла α, то точка F лежит на пересечении биссектрис треугольника, а значит, служит центром вписанной в фи-треугольник окружности. Поистине – ключевая точка!
Поскольку Obf =
OB = R, то и <OObf B = <OBF
|
1 |
2 |
3 |
4 |
5 |
6 |
|
<BOObf |
180гр - 2<OBF |
|
155,4818771 |
3α |
|
|
<Obf OO |
180 - 90 - γ |
|
51,827292373 |
α |
|
|
<AOO |
90 + γ |
|
103,654584746 |
2α |
|
|
<AOObf |
<AOO - <ObfOO |
|
51,827292373 |
α |
|
|
ObfyO |
R*cosα |
0,618033989 |
0,636009825 |
h / 2 |
|
|
EObfy |
ObfyO + EO |
0,854101966 |
0,878943961 |
|
|
|
ObfyO |
H - ObfyO |
0,381966011 |
0,393075689 |
|
|
|
H/ObfyO |
|
3,236067977 |
2Ф |
||
|
FObfy |
EObfy - EF |
0,381966011 |
0,393075689 |
ObfyO |
|
Таким образом, проекция т.Obf на ось у делит отрезок FO пополам.
|
Obf Obfy |
ObfObfy = R*sinα |
0,786151378 |
0,809016994 |
|
Ф/2 |
А что же будет,
если мы построим первую золотую линию вниз от треугольника?
Назовём её f 1', а точку - F' и отрезки - соответственно.
|
1 |
2 |
3 |
4 |
5 |
6 |
|
EF' = EF |
|
0,472135955 |
0,485868272 |
|
|
|
OF' |
EF' + OE |
0,708203932 |
0,728802408 |
|
|
|
<Of1' OF |
arccos(OF1'/R) |
0,783845351 |
44,9110304 |
|
|
|
<Of1'Ooo |
90 - <Of1'OF |
0,786950976 |
45,0889696 |
|
|
|
F' O |
EF1'+ H |
1,708203932 |
1,757887921 |
|
|
|
F' Of1' |
R*sin<Of1'OF |
0,706007925 |
0,726542528 |
|
|
|
<F'Of1'O |
arctg(F'O /F'Of1') |
1,178873651 |
67,5444848 |
|
|
Проведём линию до пересечения с окружностью BF' Of '. Заметим как само собой разумеющееся, что <EBF' = <EBF:
|
1 |
2 |
3 |
4 |
5 |
6 |
|
<EBF' |
<EBF |
0,452278447 |
25,91364619 |
|
|
|
<OBF' |
<EBF' + < γ |
0,690595909 |
39,568230932 |
= <OOf 'B |
|
|
<Of 'OB |
180 - 2<OBF' |
1,760400836 |
100,8635381 |
|
|
|
<F'OB |
90 - < γ |
1,332478865 |
76,345415254 |
2β |
|
|
<Of 'OF' |
<Of 'OB - <F'OB |
|
24,518122881 |
|
|
|
<AOOf ' |
90 - Of 'OF' - < γ |
|
51,827292373 |
α |
|
|
<Of 'OO' |
180 - 3<α |
0,427921971 |
24,51812288 |
|
|
|
<Of 'OOf |
2< Of 'OO' |
0,855843941 |
49,03624576 |
|
|
Забегая вперёд, отметим, что это весьма странный угол. И повстречается он нам ещё в самых неожиданных местах.
Итак, мы имеем по периметру окружности шесть совершенно одинаковых углов, расположенных симметрично вертикальной оси и равных:
51,827292373 град = α
и седьмой угол, направленный от центра раструбом вниз (назовем его α' ), равный 49,03624576 град и отличающийся от α на величину : дельта α = 2,791046611град
Это дает нам право построить семиугольник (темно-синий цвет), который не выглядит (визуально) неправильным.
- ВОТ ВАМ И СЕМЬ ЧАСТЕЙ ЦЕЛОГО!!!
В заключение первой части вспомним, что отрезок ОЕ = ОF. Это означает, что, если треугольник перевернуть, то его основание совпадет с первой золотой линией f.
На основе фи-треугольника в сочетании с описанной вокруг него окружностью можно получить великое множество всяких фигур, в частности: правильные многоугольники… По ходу будущего повествования мы выявим и немалое число прочих интересных закономерностей. И их, наверное, может быть бесконечно много, и для изучения требуется и мощный математический аппарат, и совершенная вычислительная техника. Поэтому будем весьма благодарны за участие в выявлении новых свойств фи-треугольника , а также за сообщения в случае обнаружения каких-либо неточностей в вычислениях. Одним словом, приглашаем Вас к творческому поиску.
Продолжение следует
Ваши комментарии к этой статье
№9 весна 2002 г дата публикации: 11.03.2002